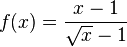اعداد اول و قضایا در باره ی این اعداد
عدد یکان اعداد اول بزرگتر از ۱۰ فقط ممکن است اعداد ۱، ۳، ۷، ۹ باشد.
پیدا کردن ضابطه ای جبری برای اعداد اول جزو یکی از معماهای ریاضی باقیمانده است و هنوز کسی به فرمولی برای آنها به دست نیاورده است.
دنبالهٔ اعداد اول به این صورت شروع میشود: ۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹ ...
قضیهها
- قضیه ۱: تعداد اعداد اول بینهایت است.
به این اثبات دقت کنیداز برهان خلف استفاده می کنیم:
فرض خلف : اعداد اول متناهی است.
اعداد اول را در هم ضرب می کنیم.
P1,P2,P3,...,Pn
ضرب اعداد از Pi بزرگتراست.






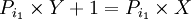
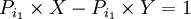
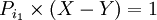
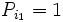
که عدد ۱ جزو اعداد اول نیست پس به تناقض می رسیم و فرض خلف باطل است. اعداد اول نامتناهی هستند.
- قضیه ۲ (قضیه اساسی حساب): هر عدد طبیعی بزرگتر از ۱ را می توان به شکل حاصلضرب اعدادی اول نوشت.
- قضیه ۳ (قضیه چپیشف):اگر n عددی طبیعی و بزرگتر از ۳ باشد، حتما" بین n و ۲n عدد اولی وجود دارد.
- قضیه ۴ هر عدد زوج را میتوان بصورت جمع دو عدد اول نوشت.
- قضیه ۵ هر عدد فرد (شامل اعداد اول) را میتوان به صورت جمع سه عدد اول نوشت (اثبات بر پایه قضیه ۴)
- قضیه ۶-هر عدد فرد را میتوان به صورت دو برابر یک عدد اول بعلاوه یک عدد اول دیگر نوشت (برهان آن را بنویسد).
خواص اعداد اول
- هر عدد اول برابر است با ۶n+۱ و ۶n-۱ که n یک عدد صحیح است.
- مجذور هر عدد اول برابر است با ۲۴n+۱.
- تفاضل مجذورهای دو عدد اول مضربی از ۲۴ است.
- حاصلضرب هر دو عدد اول بجز ۲و۳ مضربی از ۶ بعلاوه یا منهای یک است.
- توان چهارم هر عدد اول بجز ۲و۳ مضربی از ۲۴۰ بعلاوه یک است.
کشف و محاسبه
بزرگترین عدد اول کشف شده برابر دو به توان ۳۲میلیون و ۵۸۲هزار و ۶۵۷منهای یک است.این عدد یک عدد مرسن است. عدد مرسن عددی است که برابر ۲ به توان n منهای یک است.
منبع:ویکی پدیا
 است.
است.
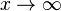 یعنی متغیر
یعنی متغیر  نمایش میدهند و میخوانند «الف صفر» (از اولین حرف
نمایش میدهند و میخوانند «الف صفر» (از اولین حرف  ) هرگاه یک
) هرگاه یک  وجود داشته باشد.
وجود داشته باشد. 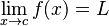
 یک
یک 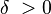 وجود دارد، که برای هر
وجود دارد، که برای هر  ، آنگاه داریم:
، آنگاه داریم:  .
.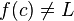 باشد. دو مثال زیر مساله را روشنتر بیان میکند.
باشد. دو مثال زیر مساله را روشنتر بیان میکند. 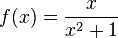 است و به x مقدار ۲ را میدهیم. در این مثال x در ۲ تعریف شده و مقدار تابع در آن برابر حدش ۰٫۴ است:
است و به x مقدار ۲ را میدهیم. در این مثال x در ۲ تعریف شده و مقدار تابع در آن برابر حدش ۰٫۴ است: 0.4
0.4 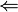
 . در این مثال
. در این مثال 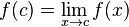 است اما این عبارت همواره صحیح نیست، برای مثال:
است اما این عبارت همواره صحیح نیست، برای مثال: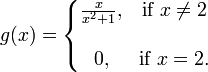
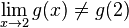 و g در ۲
و g در ۲