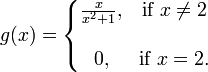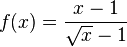مفهوم حد(یا همان limit)در ریاضیات
حد
حد در ریاضیات مفهومی است برای بیان رفتار تابع در نزدیکی یک نقطه هنگامی که متغیر تابع به آن نقطه میل میکند.
تعریف
عبارت:
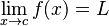
به این معنی است که، برای هر  یک
یک 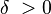 وجود دارد، که برای هر x با خاصیت
وجود دارد، که برای هر x با خاصیت  ، آنگاه داریم:
، آنگاه داریم:  .
.
حد تابع
فرض کنید f(x) تابعی حقیقی و c عددی حقیقی باشد. عبارت
بدین معناست که f(x) به ازای xهای نزدیک به c به L میل میکند. توجه داشته باشید که این عبارت میتواند صحیح باشد حتی اگر 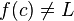 باشد. دو مثال زیر مساله را روشنتر بیان میکند.
باشد. دو مثال زیر مساله را روشنتر بیان میکند. 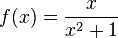 است و به x مقدار ۲ را میدهیم. در این مثال x در ۲ تعریف شده و مقدار تابع در آن برابر حدش ۰٫۴ است:
است و به x مقدار ۲ را میدهیم. در این مثال x در ۲ تعریف شده و مقدار تابع در آن برابر حدش ۰٫۴ است:
| f(1.9) | f(1.99) | f(1.999) | f(2) | f(2.001) | f(2.01) | f(2.1) |
| 0.4121 | 0.4012 | 0.4001 |  0.4 0.4 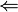 |
0.3998 | 0.3988 | 0.3882 |
اگر به x مقدار ۲ را بدهیم f(x) برابر ۰٫۴ خواهد شد و داریم  . در این مثال
. در این مثال 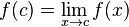 است اما این عبارت همواره صحیح نیست، برای مثال:
است اما این عبارت همواره صحیح نیست، برای مثال:
حد g(x) به ازای x برابر ۲ مساوی ۰٫۴ میباشد اما 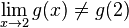 و g در ۲ پیوسته نیست.
و g در ۲ پیوسته نیست.
در مثالی دیگر فرش می کنیم که تابع در x = c تعریف نشده باشد:
اگر به x مقدار ۲ را بدهیم تابع تعریف نشده اما حد آن برابر ۲ است:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.95 | 1.99 | 1.999 |  تعریف نشده تعریف نشده 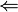 |
2.001 | 2.010 | 2.10 |