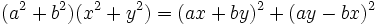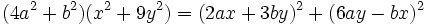اعداد تاکسی

  اعداد تاكسي چيست
زماني كه رياضيدان انگليسي هاردي براي عيادت رياضيدان شهير هند رامانوجان به
بيمارستان رفته بود به اين موضوع اشاره كرد كه شماره تاكسي كه به وسيله آن به
بيمارستان آمده، عدد بي ربط و بي خاصيت 1729 بوده است . رامانوجان بلافاصله ضمن رد
ادعاي هاردي به او يادآور شد كه اتفاقا 1729 بسيار جالب توجه است . خود ۱۷۲۹ عدد
اول است. دو عدد ۱۷ و ۲۹ هر كدام عدد اول هستند. جمع چهار رقم تشكيل دهنده آن ميشود
۱۹ كه اول است. جمع دو عدد اوليه و دو عدد آخري ميشود ۸۱۱ كه باز هم عدد اول است دو
عدد ابتدايي(سمت چپ) اگر جمع شوند؛عدد ۸۲۹ ميشود كه باز هم عدد اول است. دو عدد
اوليه اگر از هم ديگر كسر شوند؛عدد ۶۷ ساخته ميشود كه باز هم عدد اول است. سه عدد
سازنده آن عدد اول است(۱و۷و ۲). عدد اول؛عددي است كه فقط بر يك و خودش تقسيم
ميشودبنحوي كه نتيجه تقسيم عددي كسري نباشد(خارج تقسيم نداشته باشد) جمع عددي اعداد
تشكيل دهنده ۱۷۲۹ يا:۱+۷+۲+۹=۱۹ است؛ عكس ۱۹ عدد ۹۱ است؛ اگر ۱۹*۹۱بشودنتيجه برابر
۱۷۲۹ ميشود. اين هم يكي ديگر از اختصاصات ۱۷۲۹ است كه در هر عددي ديده نميشود. عدد
1729 اولين عددي است كه مي توان آنرا به دو طريق به صورت حاصلجمع مكعبهاي دو عدد
مثبت نوشت : به توان 3 به علاوه 1 به توان 3 و 10 به توان 3 به علاوه 9 به توان 3
هردو برابر 1729 مي باشند .(اولين مطلب موجود در رابطه با اين خاصيت 1729 به كارهاي
بسي رياضيدان فرانسوي قرن هفدهم باز مي گردد.) حال اگر كمي مانند رياضيدانها عمل
كنيد بايد به دنبال كوچكترين عددي بگرديد كه به سه طريق مختلف حاصلجمع مكعبهاي دو
عدد مثبت است اين عدد87539319 مي باشد كه در سال 1957توسط ليچ كشف شد: 414 به توان
3 + 255 به توان 3 و 423 به توان 3+ 228 به توان 3 و 436 به توان 3 + 167 به توان 3
هر سه جوابشان برابر 87539319 است . امروزه رياضيدانان عددي را كه به n طريق مختلف
به صورت حاصلجمع مكعبهاي دو عدد مثبت باشد ،n ــامين عدد تاكسي مي نامند و آنرا با
Taxicab نمايش مي دهند.جالبتر از همه اينكه ،هاردي و رايت ثابت كردند براي هر عدد
طبيعي n ناكوچكتر از 1 ،n ــامين عدد تاكسي وجود دارد ! هرچند، چهارمين تا هشتمين
اعداد تاكسي نيز كشف شده اند ولي تلاشها براي يافتن نهمين عدد تاكسي تاكنون نا كام
مانده است . متاسفانه اطلاعات زيادي درباره اعداد تاكسي موجود نيست . در ضمن ميتوان
مسئله را از راههاي ديگر نيز گسترش داد . مثلا همانگونه كه هاردي در ادامه داستان
فوق از رامانو جان پرسيد و او قادر به پاسخگويي نبود ، اين پرسش را مطرح كنيد:
كوچكترين عددي كه به دوطريق حاصلجمع توانهاي چهارم دو عدد مثبت مي باشد ،كدام است؟
اين عدد توسط اويلر يافت شده است :635318657 حاصلجمع توان چهارم 59 و 158 همچنين
توانهاي چهارم 133 و 134 مي باشد.

یک سوال جالب در مورد اعداد اول

هر عدد زوج (غير از 2)را مي شود بصورت جمع دو عدد اول نوشت مثل :4=2+2 يا 6=3+3 يا 8=3+5 10=3+7 و........

اين مساله يكي از جالبترين مسائل نظريه اعداد است كه تا بحال حل نشده است.

مساله ی شتر و گندم

ميخواهيم شما زحمت بکشيد و براي ما ده تن گندم را از شيراز به کرج که فاصله شان از يکديگر هزار کيلومتر است( اينطور فرض کنيد )منتقل نماييد. تنها وسيله ي نقليه اي هم که در اختيارتان خواهيم گذاشت يک شتر است اين شتر ميتواند تا يک تن گندم بر پشت خود حمل کند( تعجب نكنيد) و شب و روز راه برود. بيچاره براي اينهمه کار طاقت فرسا، خيلي هم کم توقع است و براي هر کيلومتر که راه ميرود، فقط يک کيلو گرم از گندمي را که بر پشت خود دارد ميخورد. شما براي ما حساب کنيد ببينيد با چنين شتري حد اکثر چند تن گندم را ميتوانيد در کرج تحويل ما بدهيد.

 

                               

روش سریع تفریق اعداد

مدارهاي كامپيوتر طوري تعبيه شده اند كه فقط عمل + را تشخيص داده و انجام مي دهند. و اعمالي مثل تفريق و ضرب و تقسيم را از روش + بدست مي آورند.

حال بررسي مي كنيم چگونه كامپيوتر تفاضل دو عدد را بدست مي آورد.

مثلا عبارت 243 - 396 را وارد مي كنيم كامپيوتر ابتدت متمم 9 عدد دوم را بدست مي آورد. در اين مثال متمم عددي 243 مي شود 756 .

يعني مي گوييم رقم يكان اين عدد با چند جمع شود تا 9 بدست آيد ( با 6 ) - رقم دهگان با چند جمع شود تا 9 بدست آيد ( با 5 ) - رقم صدگان با چند جمع شود تا 9 بدست آيد ( با 7)

حال عدد اولي را با متمم عدد دومي جمع كرده و 1 واحد به آن اضافه مي كنيم .

1153 = 1 + 756 + 396

در آخر رقم سمت چپ جواب را خط مي زنيم ( يعني 1 را ) و عدد باقيمانده يعني 153 جواب تفريق مي باشد.

توجه داشته باشيد ذر اين روش فقط از + استفاده كرديم.

اعداد مثلثاتی

اعداد مثلثي

1، 3، 6، 10، 15، 21 و ... بنظر شما اين اعداد چه ويژگي مشترکي دارند؟ اگر دست به قلم نشويم و شکل نکشيم و آزمايش نکنيم، فهميدن ارتباط ميان آنها کمي دشوار است. به اين رابطه ها دقت کنيد مشکل شما حل خواهد شد. به اعداد موجود در اين سري، اعداد مثلثي مي گوييم.

 

1 = 1
3= 1+2
6= 1+2+3
10= 1+2+3+4
15= 1+2+3+4+5
21= 1+2+3+4+5+6
. . .

به بيان ديگر مي توان گفت که هرعدد مثلثي تشکيل شده است از حاصل جمع يکسري از اعداد متولي طبيعي. به اين معني که اولين عدد مثلثي مساوي است با مجموع يک عدد از اعداد طبيعي، دومين معادل است با مجموع دو عدد از اعداد طبيعي، سومين معادل است با مجموع س عدد از اعداد طبيعي و ... و بالاخره n امين عدد مثلثي معادل است با مجموع n عدد از اعداد طبيعي که اگر رياضيات دبيرستان را هنوز فراموش نکرده باشيد بخاطر خواهيد آورد که مقدار اين عدد معادل n(n+1)/2 خواهد بود. (يک تصاعد ساده حسابي)

مجموع دو عدد مثلثي متوالي

اگر هر دو عدد پشت سرهم در سري اعداد مثلثي را با هم جمع کنيم حاصل جمع يک عدد مربع مي شود. مثلا" 1+3=4 يا 3+6=9 يا 6+10=16 و ... البته دليل آن ساده است به شکل دوم توجه کنيد و ببينيد که چگونه دو مثلث قرمز و سبز روي هم تشکيل يک مربع را مي دهند. (سعي کنيد با استدلال رياضي هم اين موضوع را ثابت کنيد، ساده است از همان رابطه بالا استفاده کنيد.)

مطلب اخير اغلب بصورت قضيه "مربع هر عدد طبيعي برابر است با مجموع دو عدد مثلثي متوالي" نيز مطرح مي شود.

بزرگترین عدد (عدد گوگول)

آيا ميدانيد google به چه معني است؟ Google از کلمه Googol گرفته شده است. Googol هم اسم مستعار يک عدد است که توسط «ميلتون سيروتا» نامگذاري شده است.عدد مذکور «ده به توان صد» است(به بزرگي اين عدد دقت کنيد)
انتخاب گوگل جنبه شعاري دارد.به اين مفهوم که گوگل قصد دارد تا سرويسها و خدمات و اهداف خود را به تمام جهان گسترش دهد.
به عدد «ده به توان ده به توان صد» گوگل پلکس(Googolplex) ميگويند.
و به عدد «ده به توان ده به توان ده به توان صد»گوگل دوپلکس (Googolduplex) ميگويند

توجه داشته باشيد كه عدد گوگول در تمامي كشورها كاربرد دارد . و از اين عدد به عنوان بزرگترين عدد شناخته شده كه داراي اسم مي باشد ياد مي برند.

راز عدد 19 در قران کریم

عدد ۱۹ يکي ار اعداد اولي است که زيبايهاي خاصي دارد از جمله اين زيبايها رابطه اين عدد با آيات قرآن مي باشد با توجه به اين نکات زير در مي يابيم که قرآن از ديدگاه رياضي هم معجزه اي بس عظيم است
*********************

1- اولين آيه قرآن « بسم الله الرحمن الرحيم » داراي 19 حرف عربي است.

2- قرآن از 114 سوره تشكيل شده است و اين عدد به 19 قسمت است. (6× 19).

3- اولين سوره اي كه نازل شده است سوره علق (شماره96) نوزدهمين سوره از آخر قرآن است.

4- سوره علق 19 آيه دارد.

۵- سوره علق 285 حرف (15× 19) دارد.

۶- اعداد كلمات موجود بين دو آيه بسم الله سوره النمل 342(18*19) ميباشد.

۷- قرآن مجيد شامل اعداد بيشماري است .مثلاً : ما موسي را براي جهل شب احضار كرديم ،ما هفت آسمان را آفريديم .شمار اين اعداد در تمام قرآن 285(15*19) ميباشد.

۸- اگر  285  اعداد فوق را با هم جمع كنيم ، حاصل جمع 174591 (9189*19)خواهد بود .

۹- حتي اگر اعداد تكراري را از عدد فوق حذف نماييم حاصل جمع 162146 (8534*19) خواهد بود.

۱۰- سوره قاف كه با حرف ق شروع مي شود (شماره 50 ) شامل 57(3*19) حروف ق است.

۱۱- سوره ديگري در قرآن“ حروف ق را در علامت رمزي خود دارد (سوره شورا شماره 42) كه اگر حروف ق را در اين سوره شمارش نمائيد، ملاحظه خواهيد كرد كه حرف ق 57 (3 * 19) بار تكرار شده است.

۱۲- تنها سوره اي كه با حرف « ن » آغاز ميشود ، سوره قلم است ( شماره 6 ) اين سوره 133 « ن » دارد كه به 19 قابل قسمت است ( 7×19).

۱۳- سه سوره اعراف (شماره 7 ) مريم ( شماره 19 ) و ص ( شماره 38) كه با حروف « ص» شروع ميشوند، جمعاً 152 حرف « ص » دارند ( 8×19).

۱۴- در سوره طه (شماره 20 ) جمع تعداد حروف « ط » و « هـ» 344 ميباشد ( 18 × 19) .

۱۵- در سوره « يس » تعداد حروف « ي » و « س» 285 ميباشد ( 15×19). 

۱۶- در سوره هاي شماره 2و3و7و13و19و30و31و32 كه با رمز « الم » شروع ميشوند تعداد حروف الف ، لام ، ميم جمعاً 26676 مورد و قابل قسمت به 19 ميباشند ( 1404*19).

۱۷- در سوره هاي 20و26و27و28و36و42 كه با رمز « طس » يا يكي از دو حرف مزبور (ط ، س) آغاز ميشوند تعداد دو حرف « ط » و «س» 494 مورد ميباشد ( 26*19).

۱۸- در سوره هاي 10و11و12و14و15 كه با رمز « الر» آغاز مي شوند تعدا الف ، لام ، راء به اضافه تعداد ( راء ) تنها در سوره سيزدهم ،9،97 مورد است كه اين عدد قابل قسمت بر عدد 19 مي باشد (511*19).

۱۹- در سوره هايي كه با رمز يكي از حروف “ط“ “س“ و “م“ آغاز مي شوند ، تعداد حروف طاء و سين و ميم 9177 مورد مي باشد (438*19).

۲۰- در سوره رعد ( شماره 13 ) كه با حرف رمزي “المرا“ آغاز مي شود ، تعداد حروف (الف ، لام ، ميم، را ) 1501 مورد مي باشد (79*19).

۲۱- در سوره اعراف (شماره 7) كه با حروف رمزي “المص“ شروع مي گردد تعداد وقوع “الف“ 2572 مورد ، حرف “لام“ 1523 مورد ، حرف “ميم“ 165 و حرف “ص“ 98 مورد كه جمعاً عدد 5358 بدست مي آيد(282*19).

۲۲- در سوره مريم (شماره 19) كه با حروف “كهيعص“ شروع مي شود ، تعداد حروف (كاف ، ها ، يا ، عين ، صاد) 798 مورد مي باشد (42*19).

۲۳- در سوره شورا (شماره 42) كه با حروف “حم عسق “ شروع مي شود ، تعداد حروف (حا ، ميم ، عين، سين ، قاف ) 570 مورد مي باشد(30*19).


۲۴- در سيزده سوره اي كه حرف “الف“ در لغت رمزي آنهاست (سوره هاي شماره 2 ، 3 ، 7 ، 10 ، 11 ، 12 ، 13 ، 14 ، 29 ، 30 ، 31 ، 32و15 ) جمع الف هاي موجود 17499 مورد مي باشد(921*19).

۲۵- در سيزده سوره فوق الذكر جمع حروف “لام“ 1870 مورد مي باشد(620*19).

۲۶- در هفده سوره اي كه حروف “ميم“ در لغت رمزي آنها ست (سوره هاي شماره 2 ، 3 ، 7 ، 13 ، 32 ، 26 ، 28 ، 29 ، 31 ، 30 ، 40 ، 41 ، 42 ، 43 ، 44 ، 45 ، 46 ) جمع حروف “ميم“ 8683 مورد مي باشد (457*19).

براستي آيا قرآن مجيد معجزه اي بس عظيم نيست!؟

معمایی عجیب؟

 يه آمار گير ميره در يه خونه اي و راجع به خودش و بچه هاش سوال ميکنه.
طرف ميگه: "براي سن بچه هام يه معما ميگم بايد حلش کني تا سنشون رو پيدا کني. من سه پسر دارم که حاصل ضرب سن اونا ميشه 36 و حاصل جمع سنشون 2 تا از شماره پلاک همسايه سمت راستي کمتره".
آمار گيره يه خورده فکر ميکنه و ميگه: "با اين اطلاعات نميتونم حلش کنم ميشه يه راهنمايي بکنين".
صابخونه ميگه: "پسر بزرگترم ماكاروني خيلي دوست داره!!!" و آمارگيره مساله رو حل ميکنه!!
حالا شما ميتونين بگين سن بچه ها به ترتيب چند بوده؟!!

تاریخچه ی عدد صفر(0)

 يکي از معمول ترين سوال هايي که مطرح ميشود اين است که: چه کسي صفر را کشف کرد ؟ البته براي جواب دادن به اين سوال به دنبال اين نيستيم که بگوييم شخص خاصي صفر را ابداع کرد و ديگران از آن زمان به بعد از آن استفاده ميکردند.

     اولين نکته شايان ذکر در مورد عدد صفر اين است که اين عدد دو کاربرد دارد که هر دو بسيار مهم تلقي مي شود. يکي از کاربرد هاي عدد صفر اين است که به عنوان نشانه اي براي جاي خالي در دستگاه اعداد (جدول ارزش مکاني اعداد) به کار مي رود. بنابر اين در عددي مانند ۲۱۰۶ عدد صفر استفاده شده تا جايگاه اعداد در جدول مشخص شود که به طور قطع اين عدد با عدد ۲۱۶ کاملا متفاوت است. دومين کاربرد صفر اين است که خودش به عنوان عدد به کار مي رود که ما به شکل عدد صفر از آن استفاده مي کنيم.

    هيچکدام از اين کاربرد ها تاريخچه پيدايش واضحي ندارند. در دوره اوليه تاريخ کاربرد اعداد بيشتر به طور واقعي بوده تا عصر حاضر که اعداد مفهوم انتزاعي دارند. به طور مثال مردم دوران باستان اعداد را براي شمارش تعداد اسبان، ...به کار مي بردند و در اين گونه مسايل هيچگاه به مساله اي برخورد نمي کردند که جواب آن صفر يا اعداد منفي باشد.

    بابلي ها تا مدتها در جدول ارزش مکاني هيچ نمادي را براي جاي خالي در جدول به کار نمي بردند. مي توان گفت از اولين نمادي که آنها براي نشان دادن جاي خالي استفاده کردند گيومه (") مثلا عدد ۶"۲۱ نمايش دهنده ۲۱۰۶ بود. البته بايد در نظر داشت که از علا‌‌ئم ديگري نيز براي نشان دادن جاي خالي استفاده مي شد وليکن هيچگاه اين علائم به عنوان آخرين رقم آورده نمي شدند بلکه هميشه بين دو عدد قرار مي گرفتند. به طور مثال عدد "۲۱۶ را با اين گونه علامت گذاري نداريم. به اين ترتيب به اين مطلب پي مي بريم که کاربرد اوليه عدد صفر براي نشان دادن جاي خالي اصلا به عنوان يک عدد نبوده است.

     البته يونانيان هم خود را از اولين کساني مي دانند که در جاي خالي از صفر استفاده مي کردند. اما يونانيان دستگاه اعداد (جدول ارزش مکاني اعداد) مثل بابليان نداشتند. اساسا دستاورد هاي يونانيان در زمينه رياضي بر مبناي هندسه بوده و به عبارت ديگر نيازي نبوده است که رياضيدانان يوناني از اعداد نام ببرند؛ زيرا آنها اعداد را به عنوان طول خط مورد استفاده قرار ميدادند.

     البته بعضي از رياضيدانان يوناني ثبت اطلاعات نجومي را بر عهده داشتند. در اين قسمت به اولين کاربرد علامتي اشاره مي کنيم که امروزه آن را به اين دليل که ستاره شناسان يوناني براي اولين بار علامت  0 را براي آن اتخاذ کردند، عدد صفر مي ناميم. تعداد معدودي از ستاره شناسان اين علامت را به کار بردند و قبل از اين که سر انجام عدد صفر جاي خود را به دست آورد، ديگر مورد استفاده قرار نگرفت و سپس در رياضيات هند ظاهر شد.

     هنديان کساني بودند که پيشرفت چشمگيري از اعداد و جدول ارزش مکاني اعداد ايجاد کردند. هنديان نيز از صفر براي نشان دادن جاي خالي در جدول استفاده مي کردند.

     اکنون اولين حضور صفر را به عنوان يک عدد مورد بررسي قرار مي دهيم: اولين نکته اي که مي توان به آن اشاره کرد اين است که صفر به هيچ وجه نشان دهنده يک عدد به طور معمول نمي باشد. از زمان هاي پيش اعداد به مجموعه اي از اشياء نسبت داده مي شدند و در حقيقت با گذشت زمان مفهوم صفر و اعداد منفي که از ويژگي هاي مجموعه اشياء نتيجه نمي شدند، ممکن شد. هنگامي که فردي تلاش مي کند تا صفر و اعداد منفي را به عنوان عدد در نظر بگيرد با اين مشکل مواجه مي شود که اين عدد چگونه در عمليات محاسباتي جمع، تفريق، ضرب و تقسيم عمل ميکند. رياضيدانان هندي سعي بر آن داشتند تا به اين سوالات پاسخ دهند و در اين زمينه نيز تا حدودي موفق بوده اند.

      اين نکته نيز قابل ذکر است که تمدن ماياها که در آمريکاي مرکزي زندگي مي کردند نيز از دستگاه اعداد استفاده مي کردند و براي نشان دادن جاي خالي صفر را به کار مي بردند.

      بعد ها نظريات رياضيدانان هندي علاوه بر غرب، به رياضيدانان اسلامي و عربي نيز انتقال يافت. فيوناچي، مهم ترين رابط بين دستگاه اعداد هندي و عربي و رياضيات اروپا مي باشد.

یک عدد عجیب

يک نفر از اساتيد دانشکده شهر آتن پايتخت يونان چندي پيش عددي را کشف کرد که خصايص عجيبي دارد.
آن عدد:142857 ميباشد.
اگر عدد مذکور را در دو ضرب کنيم، حاصل: 285714 ميشود! (به ارزش مکاني 14 توجه کنيد).
اگر اين عدد را در سه ضرب کنيم حاصل: 428571 ميشود!(به ارزش مکاني 1 توجه کنيد).
اگر اين عدد را در چهار ضرب کنيم حاصل: 571428 ميشود!( به ارزش مکاني 57 توجه کنيد).
اگر اين عدد را در پنج ضرب کنيم حاصل: 714285 ميشود!(به ارزش مکاني 7 توجه کنيد).
اگر اين عدد را در شش ضرب کنيم حاصل: 857142 ميشود! (سه رقم اول با سه رقم دوم جا بجا شده)
اگر اين عدد را در هفت ضرب کنيم حاصل: 999999 ميشود!
لطفا" ضربهاي بالا را خود شما نيز انجام دهيد و حاصل را با عدد اصلي مقايسه کنيد.

اثبات علمی 64=65

با توجه به شكل 65 با 64 برابر است.

نظر شما درباره اين اثبات چيست

یک سوال زیبای هندسه

      

مثلث راستگوشه اي با ابعاد  ۵ و ۱۲ و ۱۳ در يک مربع محاط شده است. طول دقيق ضلع مربع يا مساحت آنرا  بدست آوريد.

مقدار X را دقیقا بدست اورید

مسئله را در حالت کلي که طول اضلاع مثلث a و b و c باشد نيز حل نماييد و مساحت مربع را بر حسب اين سه پارامتر معلوم سازيد.

 

 

پاسخ خودم به این سوال رو می توانید در ادامه ی مطلب بخوانید.

ادامه نوشته

روش فوق سریع ضرب ذهنی

در قسمت آرشيو روشهاي در مورد ضرب ذهني بيان شد. در اين قسمت نيز يك روش فوق العاده سريع بيان ميكنيم.

هرگاه بخواهيم عددي دلخواه را در عدد دلخواه ديگر ( البته تمام ارقامش 9 باشد ) ضرب كنيم . از روش زير مي توان اين كار را انجام داد.

ما با يك مثال اين روش را بيان مي كنيم .

مي خواهيم عدد 247 را در عدد 999 ضرب نماييم.

ابتدا رقم يكانها را در هم ضرب كرده و با فاصله آنها را نوشته و بين آن وپشت آن دو خط تيره رسم مي كنيم .

                                       3--6--

حال به رقم دهگان يك واحد اضافه كرده و آنرا در 9 ضرب كرده و رقم يكان جواب را سمت چپ 3 و رقم دهگان را سمت چپ 6 مي نويسيم.

                                      53-46-

حال نوبت رقم صدگان مي رسد . يك واحد به رقم صدگان اضافه كرده آنرا در 9 ضرب مي كنيم . رقم يكان جواب را سمت چپ 5 و رقم دهگان را سمت چپ 4 مي نويسيم .

                                     246753

بدين ترتيب جواب اين ضرب عدد 246753 مي شود.

جالب اينكه اين روش منسوب به يك پسر بچه 10 ساله مي باشد

شگفتی عدد 312

اگر اين قسمت را بخوانيد برايتان جالب خواهد بود و بيشتر به رياضي علاقمند مي شويد.

هر عددي دوست داريد در نظر بگيريد ( مثلا عدد 674328 )

تعداد رقمهاي اين عدد را شمرده و آنرا بنويسيد ( در اين مثال 6 مي شود )

سپس تعداد ارقام زوج را شمرده کنار عدد قبلي قرار دهيد ( تعداد زوجها 4 است پس داريم 64 )

حال تعداد ارقام فرد را شمرده کنار عدد قبلي قرار دهيد ( تعداد فردها 2 است پس داريم 642 )

هم اکنون عدد 642 را داريم با اين عدد نيز مراحل با لا را تکرار کرده

تعداد رقمهاي اين عدد را شمرده و آنرا بنويسيد ( 3 مي شود )

سپس تعداد ارقام زوج را شمرده کنار عدد قبلي قرار دهيد ( تعداد زوجها 3 است پس داريم 33 )

حال تعداد ارقام فرد را شمرده کنار عدد قبلي قرار دهيد ( تعداد فردها 0 است پس داريم 330 )

حالا براي عدد 330 اين کار را انجام مي دهيم

تعداد رقمهاي اين عدد را شمرده و آنرا بنويسيد ( 3 مي شود )

سپس تعداد ارقام زوج را شمرده کنار عدد قبلي قرار دهيد ( تعداد زوجها 1 است پس داريم 31)

حال تعداد ارقام فرد را شمرده کنار عدد قبلي قرار دهيد ( تعداد فردها 2 است پس داريم 312 )

در اين مثال مشاهده نموديم که آ خر به 312 رسيديم

ما ادعا مي کنيم که هر عدد طبيعي با اين روال به 312 ختم مي شود باور نداريد امتحان کنيد.

مثلث خیام پاسکال

مثلث خیام ، پاسکال

بسیاری عقیده دارند که مثلث حسابی پاسکال را باید مثلث حسابی خیام نامید و برخی پا را از این هم فراتر گذاشته اند و معتقد اند که دو جمله ای نیوتون را باید دوجمله ای خیام نامید . اندکی در این باره دقت کنیم.

همه کسانی که با جبر مقدماتی آشنایی دارند ،"دستور نیوتن" را درباره بسط دوجمله ای میشناسند. این دستور برای چند حالت خاص (وقتی n عددی درست و مثبت باشد) چنین است:

(a+b)⁰ = 1 (1)
(a+b)¹ = a+b (1,1)
(a+b)² = a²+2ab+b² (1,2,1)
(a+b)³ = a³+3a²b+3ab²+b³ (1,3,3,1)
(a+b)⁴ = a⁴+4a³b²+6a²b²+4a²b³+b⁴ (1,4,6,4,1)
. . .

اعداد داخل پرانتزها، معرف ضریبهای عددی جمله ها در بسط دوجمله ای است.

بلیز پاسکال (Blaise Pascal) فیلسوف و ریاضی دان فرانسوی که کم وبیش با نیوتون همزمان بود، برای تنظیم ضریبهای بسط دوجمله ای، مثلثی درست کرد که امروز به "مثلث حسابی پاسکال" مشهور است. طرح این مثلث برای نخستین بار در سال 1665 میلادی در "رساله مربوط به مثلث حسابی "چاپ شد.مثلث حسابی چنین است:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1

دراین مثلث از سطر سوم به بعد هر عددبرابر با مجموع اعداد بالا و سمت چپ آن در سطر قبل است و بنابراین میتوان آنرا تا هر جا که للازم باشدادامه داد. هرسطر این مثلث ضریبهای بسط دوجمله ای را در یکی از حالتها بدست میدهد بطوری که n همان شماره سطر باشد.

ضریبهای بسط دوجمله ای (برای توانهای درست و مثبت) حتا در سده دوم پیش از میلاد البته به صورت کم و بیش مبهم برای دانشمندان هندی روشن بوده است .باوجود این حق این است که دستور بسط دو جمله ای با نام نیوتن همراه باشد زیرا نیوتن آن را برای حالت کلی و وقتی n عددی کسری یا منفی باشد در سال 1676میلادی بکاربرد.که البته در این صورت به یک رشته بی پایان تبدیل میشود.

اما در باره مثلث حسابی وضریبهای بسط دوجمله ای در حالت طبیعی بودن n. از جمله، دستور بسط دو جمله ای را میتوان در "کتاب حساب مخفی" میخائیل شتیفل جبردان آلمانی (که در سال 1524 چاپ شد) پیدا کرد.

در سال 1948 میلادی،پاول لیوکی آلمانی،مورخ ریاضیات،وجود دستور نیوتن را برای توانهای طبیعی ،دز کتاب "مفتاح الحساب"(1427 میلادی) غیاث الدین جمشید کاشانی کشف کرد. بعدها س.آ.احمدوف ،مورخ ریاضیات و اهل تاشکند، دستور نیوتون وقانون تشکیل ضریبهای بسط دوجمله ای را،در یکی از رساله های نصر الدین توسی،ریاضیدان بزرگ سده سیزدهم میلادی ،کشف کرد (این رساله توسی درباره محاسبه بحث میکند). چه جمشید کاشانی وچه نصرالدین توسی ،این قاعده را ضمن بررسی قانون های مربوط به ریشه گرفتن از عددها آورده اند.

همچنین براساس آگاهی هایی که داریم حکیم عمر خیام رساله ای داشته که خود رساله تاکنون پیدا نشده ولی از نام آن "درستی شیوه های هندی در جذر وکعب "اطلاع داریم ،کهدر آن به تعمیم قانونهای هندی درباره ریشه دوم و سوم ،برای هر ریشه دلخواه پرداخته.لذا خیام از "دستور نیوتن" اطلاع داشته.

اما بنا به اسناد تاریخی معتبر قانونهای مربوط بهضریبهای بسط دوجمله ای وطرح مثلث حسابی تا سده دهم میلادی(برابر چهارم هجری) جلو میرود و به کرجی (ابوبکر محمد بن حسن حاسب کرجی ریاضیدان سده ده و یازده میلادی) پایان میپذیرد .بنابراین حتی" مثلث حسابی پاسکال" را هم از نظر تاریخی نمیتوان "مثلث حسابی خیام " نامید

منبع:http://www.senmerv.com

نام اعداد خیلی بزرگ

در اینجا نام اعداد خیلی بزرگ رو گذاشتم:

بيليون = 10به توان 9
تريليون =10 به توان 12
كوادريليون =10 به توان 15
كونيتيليون =10 به توان 18
سیكستيليون =10 به توان 21
سپتيليون =10 به توان 24
اكتيليون =10 به توان 27
نونيليون =10 به توان 30
دسيليون =10 به توان 32
اندسيليون =10 به توان 36
ديودسيليون =10 به توان 39
تري دسيليون =10 به توان 42
كوتوارد دسيليون =10 به توان 45
كواين دسيليون =10 به توان 48
سیكس دسيليون =10 به توان 51
سپتن دسيليون =10 به توان 54
اكتودسيلين =10 به توان 57
نووم دسيليون =10 به توان 60
ويجنيتيليون = 10 به توان 61

تاریخچه ی عدد p(پی)

تاريخچه ي عدد p :

 

عدد p (پي) سرگذشتي حداقل 3700 ساله دارد. پي يكي از مشهور ترين عددها در دنياي رياضي است. و نماد p يكي از حروف الفباي لاتين است.ساده ترين و بهترين راه معرفي p اين است :

قطر دايره/محيط دايره = p

 

در طول اين 37 قرن، دانشمندان زيادي سعي كردند مقدار p را حساب كنند. به عبارت ديگر آن ها سعي كردند تا نزديك ترين عدد به عدد p را به دست آورند.

قديمي ترين محاسبه ي به دست آمده، به 1700 سال پيش از ميلاد مسيح (ع) ، يعني حدود 3700 سال پيش مربوط مي شود. اين محاسبات روي پاپيروسي نوشته شده است كه در حال حاضر، در "مسكو" نگهداري مي شود.

 

اولين محاسبه ي رياضي p ، توسط ارشميدس و با كمك چند ضلعي ها انجام شد. او با 96 ضلعي منتظم، عدد پي را بين دو كسر 70/10 ‚3 و71/10 ‚3 به دست آورد .(تذكر:علامت / نشانه ي خط كسري است).

 

"لودلف وان كولن" آلماني ، در قرن هفدهم به كمك 720 ‚254 ‚212 ‚32 ضلعي منتظم، مقدار p را تا 32 رقم اعشار حساب كرد.

 

"غياث الدين جمشيد كاشاني" معروف به "الكاشي" در كتاب رساله ي محيطيه، p را تا 17 رقم پس از مميز حساب كرده است.

 

"بهاسيك هندي" در سال 1150 ميلادي، آن را به صورت كسر 7/22 يا جذر 10 نشان داده است.

"جان وايس" رياضي دان انگليسي براي p ، نسبت زير را پيشنهاد كرد:

 

(...×5×5×3×3×1×1 ) / (...×6×6×4×4×2×2) = 2/p

 

"لايپ نيتس " آلماني به عبارت زير دست يافت :

 

...+۱/۱۱-۱/۹+۱/۷-۱/۵+۱/۳-۱=۴/p

 

در سال 1949 ميلادي، به كمك رايانه ي اينياك ، پي تا 2037 رقم محاسبه شد. به تازگي برادران "چودنوفسكي" با بيش از پنج سال كار مداوم به كمك رايانه، p را تا 1011196691 رقم اعشار حساب كرده اند .

 

اگر مي خواهيد عدد p را تا ده رقم اعشار به خاطر بسپاريد تعداد حروف كلمات،  در بيت دوم اين شعر به شما كمك خواهد كرد :

 

گر كسي از تو بپرسد ره آموختن p     پاسخي ده كه هنرمند تو را آموزد

خرد    و دانش و آگاهي  دانشمندان     ره  سرمنزل   مقصود  بما آموزد

۳    .  ۱     ۴     ۱        ۵            ۹             ۲       ۶          ۵        ۳      ۵              =۳/۱۴۱۵۹۲۶۵۳۵

هندسه ی فضایی

 

هندسه ی فضايي

 

مطالعه ي خواص هندسي اشياي سه بعدي امكان مناسبي براي تأكيد بر اهداف اجرايي هندسه فراهم مي آورد. مانند توصيف و دسته بندي، ساختن، كشف كردن و مرتبط ساختن شكل هاي سه بعدي با اشكال دوبعدي.

 اگر حجم هاي آماده در اختيار نداريد بايد مدل ها را بسازيد. همچنين بايد به كمك دانش آموزان تان اشياي واقعي را كه داراي شكل هاي هندسي خاصي  هستند، نظير توپ، قوطي كنسرو، جعبه هاي مخروطي و مكعبي و اشكال هندسي غير معمول ، جمع آوري كنيد.

توصيف و دسته بندي

 

بچه ها بايد قادر باشند خواص اشياي سه بعدي را توصيف كنند و تشخيص دهند كه دو يا چند شكل از چه نظر به هم شباهت دارند و يا با هم متفاوتند.توصیف و دسته بندی،روند هایی است که با اضافه کردن خواص جدید تر و پیچیده تر،تغییر می کندو کامل تر می شود.در فعالیت هایی که در زیر ارائه می شود.مجموعه ی دانستنی ها و خواصی را که مناسب دانش آموزان مبتدی،متوسط و پیشرفته است،پیشنهاد می کنیم.

ما اغلب به داتش آموزان فقط نام شکل های هندسی را می آموزیم،اما چیزی که آنان نیاز دارند،نام همراه با مفهوم و معنی است.همچنین باید قدرت تفکیک و تشخیص آنان را تقویت کنیم در این فعالیت ها ما باید مجموعه دانستنی های دانش آموزان را با اضافه کردن کلمات جدید و مناسب شکل دهیم و تکمیل کنیم.

 

فعالیت1- چند شیء را به بچه ها نشان دهید(یک استوانه ،کره،هرم و ...)سپس یکی از آن ها را تو صیف کنیدواز بچه ها بخواهید که بگویند شما کدام شیء را توصیف کردید.

 

فعالیت2- دو جسم هندسی را در دست بگیرید و از بچه ها بخواهید که بگویند این دو چه شباهت ها و چه تفاوت هایی دارند.

 

فعالیت3- سه شیء مختلف مانند استوانه ،مکعب و مخروط تهیه نمایید و از دانش آموزان بخواهید که بگویند کدام یک با دو تای دیگر متناسب نیست و چرا؟

 

فعالیت4- یک وجه عبارت است از یک سطح جانبی مسطح و صاف. از بچه ها بخواهید که تعداد وجوه اشیاء را بشمارند.

 

فعالیت5- مدلی از اشیای سه بعدی را به بچه ها نشان دهید و از آنان بخواهید که اشیای واقعی را که شبیه به آن هستند، پیدا کنند.

 

فعالیت6- بررسی یال ها،رئوس و وجوه : بعد از تعریف یال ،رأس و وجه از بچه ها بخواهید که این چیستان ها را حل کنند:

جسمی هستم با هشت یال،اسم من چیست؟

شش یال و چهار وجه،اسم من چیست؟

پنج گوشه دارم،اسم من چیست؟

تعداد گوشه ها و وجوهم با هم برابر است،اسم من چیست؟

بدون وجه و گوشه هستم،اسم من چیست؟

 

فعالیت 7- جستجوی اجسام : یک مجموعه ازفعالیت ها را ترتیب دهید که از طریق آن، بچه ها بتوانند اجسامی را مطابق با اندازه، شکل وجوه و طول یال ها جستجو کنند. سوالاتی که باید از بچه ها بپرسیدبستگی به هر جسم دارد.

به عنوان مثال اجسامی را پیدا کنید که :

1- فقط دو وجه هم شکل و هم اندازه (قابل انطباق) دارد.

2- فقط سه وجه هم شکل و هم اندازه دارد.

3- همه ی یال های آن یک طول دارند.

4- یال های آن دارای سه طول متفاوت هستند

 

 

منبع:http://math-teachers.blogfa.com

فرمول نسبت های مثلثاتی

1. sin4+cos4=1-2(sin2×cos2)

2. sin6+cos6=1-3(sin2×cos2)

3. 1-2(sin×cos)=(sin-cos)2

4. tg ×cot =1

5. sec=1/cos → sec2=1/cos2=1+tg2

6. csc=1/sin → csc2=1/sin2 =1+cot2

7. sin2+cos2=1 → sin2=1-cos2 → cos2=1-sin2

8. tan+cot=1/(sin×cos)=sec ×csc

9. sin(a ± b)=sin(a)cos(b)±sin(b)cos(a)

10. cos(a+b)=cos(a)cos(b) - sin(a)sin(b)

11. cos(a - b)=cos(a)cos(b)+sin(a)sin(b)

12. cos(a - b)×cos(a +b)=cos2a - sin2b

13. sin(a +b)×sin(a - b)=sin2a - sin2b

14. tan(a+b)=( tan(a) + tan(b) ) / ( 1-tan(a)×tan(b) )

15. tan(a - b)=( tan(a) -tan(b) ) / ( 1+tan(a)×tan(b) )

16. cot(a+b)=( cot(a)×cot(b) - 1)/( cot(a)+cot(b) )

17. cot(a - b)=( cot(a)×cot(b) +1)/( cot(a) - cot(b) )

 

منبع:http://abdenean.blogfa.com

اتحاد های جبری

مقدمه و معرفی

---

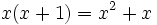در ریاضیات اتحادها تساوی هایی هستند که به ازای هر مقدار عددی از دامنه خود که بجای متغییرهایشان قرار دهیم همواره برقرار باشند. به عنوان مثال تساوی برای هر x عضو دامنه برقرار است. لذا این عبارت جبری یک اتحاد است، اما تساوی 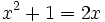فقط برای x=1 برقرار است. پس این عبارت یک اتحاد نمی باشد. در واقع در مورد یک اتحاد در اصل به یک تساوی بدیهی چون 0=0 می رسیم.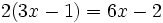
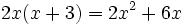
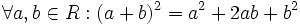
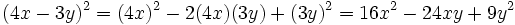
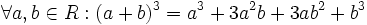
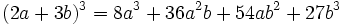
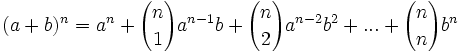
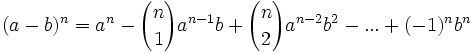
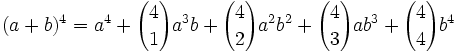
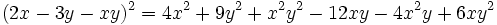
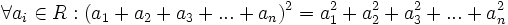
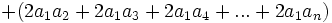
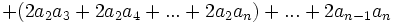
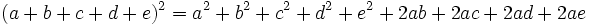
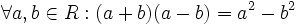
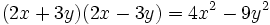
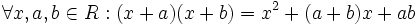
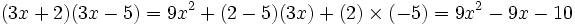
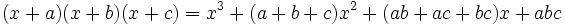
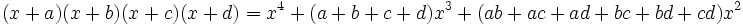
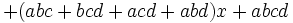
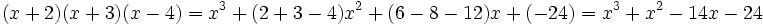
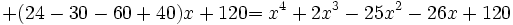
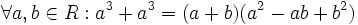
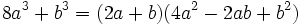
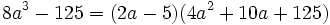
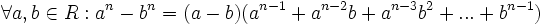
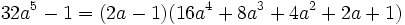
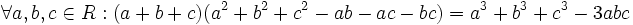
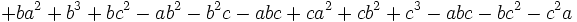
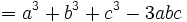
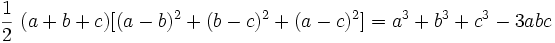
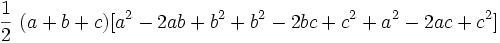
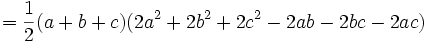
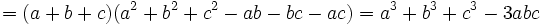
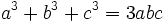
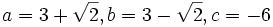به عنوان مثال در اتحاد مثال زده شده دو طرف ساده شده و تساوی 0=0 حاصل می شود.
به این ترتیب تفاوت میان یک اتحاد جبری و یک معادله جبری در این است که اتحاد جبری به ازای همه مقادیر دامنه برقرار است در صورتی که یک معادله جبری به ازای تعداد محدودی از اعضای دامنه(مجموعه جواب معادله) برقرار است.
عبارات زیر نمونه ای از اتحاد است:

اتحادهای مهم جبری

---

در میان اتحادهای جبری، برخی از اتحادها بسیار مهم و کاربردی می باشند و در حل معادلات، محاسبات جبری، تجزیه عبارت جبری و... بسیار کاربرد دارند. از این رو دانستن و به کاربردن آنها از اهمیت خاصی برخوردار است. در این قسمت به بررسی این اتحادهای مهم می پردازیم.

اتحاد مربع مجموع دو جمله

---

مثال:

اتحاد مربع تفاضل دو جمله

---

مثال:

اتحاد مکعب مجموع دو جمله

---

مثال:

اتحاد بسط دو جمله ای نیوتن

در دو اتحاد قبل مشاهدی کردید که عبارت مجموع با تفاضل دو جمله چون (a+b)،(a-b) به توان های دو و سه رسیدند. حال این اتحاد برای توانهای طبیعی n هم قابل تعمیم است و به آن اتحاد بسط دو جمله ای نیوتن می گویند.

---

مثال:

اتحاد مربع سه جمله

---

مثال:

تعمیم اتحاد مربع چند جمله

---

مثال:

اتحاد مزدوج

---

مثال:

• لازم به توضیح است اگر داشته باشیم a+b آنگاه عبارت a-b را مزدوج عبارت اول یعنی a+b می گویند.

اتحاد جمله مشترک

---

مثال:

تعمیم اتحاد جمله مشترک

• این روال به همین ترتیب برای حالات دیگر هم برقرار است.

---

مثال:

اتحاد مجموع مکعبات دو جمله(اتحاد چاق و لاغر)

---

مثال:

تعمیم اتحاد مجموع مکعبات دو جمله(اتحاد چاق و لاغر)

پس می توان نتیجه زیر را بیان کرد:

• لازم به توضیح است که این اتحاد فقط برای حالتی برقرار ست که توان n عدد طبیعی فرد باشد.

---

مثال:

اتحاد تفاضل مکعبات دو جمله(اتحاد چاق و لاغر)

---

مثال:

تعمیم اتحاد تفاضل مکعبات دو جمله(اتحاد چاق و لاغر)

پس می توان نتیجه زیر را بیان کرد:

• لازم به توضیح است این این اتحاد برای هر عدد طبیعی n برقرار است.

---

مثال:

اتحاد اویلر

• برهان:

• صورتی دیگر از اتحاد اویلر:

• برهان:

• نتایج اتحاد اویلر:
  • اگر a+b+c=0 آنگاه
  • اگر a=b=c آنگاه

---

مثال:

همچنین اگر باشد آنگاه داریم:

اتحاد لاگرانژ

---

مثال:

 

منبع:http://daneshnameh.roshd.ir